Physics of Enzyme Arrangement
Optimal spatial allocation of enzymes as an investment problem

Cells face various allocation problems demanding decisions on how to distribute their finite resources. They decide which enzymes to produce at what quantity, but also where to position them. Here we focus on the spatial allocation problem of arranging enzymes such as to maximize the total reaction flux produced by them in a system with given geometry and boundary conditions. We derive an optimal allocation principle demanding that the available enzymes are distributed such that the marginal flux returns at each occupied position are equal. This ‘homogeneous marginal returns’ (HMR) criterion corresponds to a portfolio optimization of investments that globally feed back onto all payoffs. The HMR criterion allows us to analytically understand and characterize a localization-delocalization transition in the optimal enzyme distribution. Our analysis reveals the generality of the transition, and produces a practical test for the optimality of enzyme clustering by comparing the reaction flux to the influx of substrate. Based on these results, we devise an additive construction scheme, which builds up optimal enzyme arrangements systematically rather than by trial and error. Taken together, we identify a common principle in allocation problems from biology and economics, which also serves as a design principle for synthetic biomolecular systems.
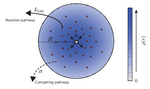
Trade-offs and design principles in the spatial organization of catalytic particles
Catalytic particles are spatially organized in a number of biological systems across different length scales, from enzyme complexes to metabolically coupled cells. Despite operating on different scales, these systems all feature localized reactions involving partially hindered diffusive transport, which is determined by the collective arrangement of the catalysts. Yet it remains largely unexplored how different arrangements affect the interplay between the reaction and transport dynamics, which ultimately determines the flux through the reaction pathway. Here we show that two fundamental trade-offs arise, the first between efficient inter-catalyst transport and the depletion of substrate, and the second between steric confinement of intermediate products and the accessibility of catalysts to substrate. We use a model reaction pathway to characterize the general design principles for the arrangement of catalysts that emerge from the interplay of these trade-offs. We find that the question of optimal catalyst arrangements generalizes the well-known Thomson problem of electrostatics.
Cross-diffusion induced patterns for a single-step enzymatic reaction
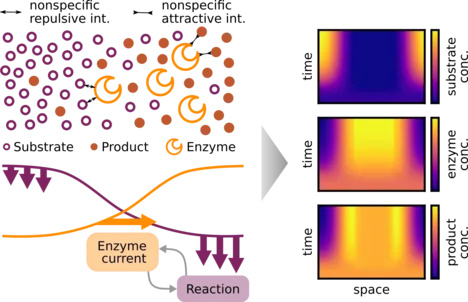
Several different enzymes display an apparent diffusion coefficient that increases with the concentration of their substrate. Moreover, their motion becomes directed in substrate gradients. Currently, there are several competing models for these transport dynamics. Here, we use mathematical modeling and numerical simulations to analyze whether the enzymatic reactions can generate a significant feedback from enzyme transport onto the substrate profile. We find that this feedback can generate spontaneous spatial patterns in the enzyme distribution, with just a single-step catalytic reaction. However, patterns are formed only for a subclass of transport models. For such models, nonspecific repulsive interactions between the enzyme and the substrate, or attractive interactions between the enzyme and the product, cause the enzyme to accumulate in regions of low substrate concentration. Reactions then amplify local substrate and product fluctuations, causing enzymes to further accumulate where substrate is low. Experimental analysis of this pattern formation process could discriminate between different transport models.
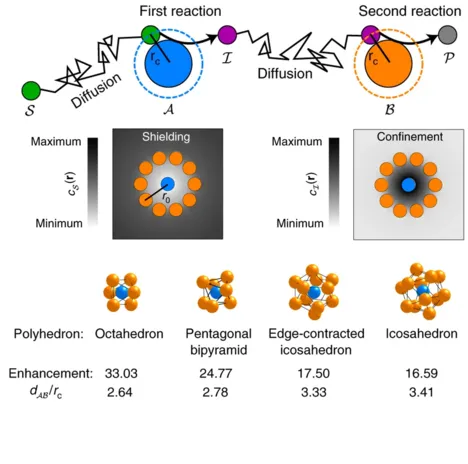
Regulation of reaction fluxes via enzyme sequestration and co-clustering

Experimental observations suggest that cells change the intracellular localization of key enzymes to regulate the reaction fluxes in enzymatic networks. In particular, cells appear to use sequestration and co-clustering of enzymes as spatial regulation strategies. These strategies should be equally useful to achieve rapid flux regulation in synthetic biomolecular systems. Here, we leverage a theoretical model to analyse the capacity of enzyme sequestration and co-clustering to control the reaction flux in a branch of a reaction–diffusion network. We find that in both cases, the response of the system is determined by two dimensionless parameters, the ratio of total activities of the competing enzymes and the ratio of diffusion to reaction timescales. Using these dependencies, we determine the parameter range for which sequestration and co-clustering can yield a biologically significant regulatory effect. Based on the known kinetic parameters of enzymes, we conclude that sequestration and co-clustering represent a viable regulation strategy for a large fraction of metabolic enzymes, and suggest design principles for reaction flux regulation in natural or synthetic systems.
more
Optimal Compartmentalization Strategies for Metabolic Microcompartments
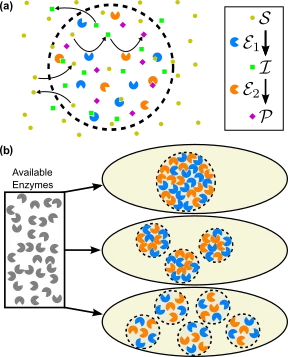
Intracellular compartmentalization of cooperating enzymes is a strategy that is frequently used by cells. Segregation of enzymes that catalyze sequential reactions can alleviate challenges such as toxic pathway intermediates, competing metabolic reactions, and slow reaction rates. Inspired by nature, synthetic biologists also seek to encapsulate engineered metabolic pathways within vesicles or proteinaceous shells to enhance the yield of industrially and pharmaceutically useful products. Although enzymatic compartments have been extensively studied experimentally, a quantitative understanding of the underlying design principles is still lacking. Here, we study theoretically how the size and enzymatic composition of compartments should be chosen so as to maximize the productivity of a model metabolic pathway. We find that maximizing productivity requires compartments larger than a certain critical size. The enzyme density within each compartment should be tuned according to a power-law scaling in the compartment size. We explain these observations using an analytically solvable, well-mixed approximation. We also investigate the qualitatively different compartmentalization strategies that emerge in parameter regimes where this approximation breaks down. Our results suggest that the different sizes and enzyme packings of α- and β-carboxysomes each constitute an optimal compartmentalization strategy given the properties of their respective protein shells.
Optimal arrangements of enzymes
We study how the spatial arrangement and coordination of enzymes determines the efficiency of a multi-step reaction. These spatial arrangements can be natural (as in biomolecular complexes) or engineered with the modern methods of bio-nanotechnology. In both cases, fundamental functional tradeoffs emerge, which must be characterized to understand the optimization of such systems. more...