Welcome to the Gerland group -
Physics of Complex Biosystem
Vision
In physics, interactions between particles follow laws. In biology, interactions between biomolecules serve a function. These very different points of view are beginning to merge as research over the past years has demonstrated how, in some exemplary cases, the laws of physics constrain the implementation of biological function.
We investigate several such cases. For instance, we study how the spatial arrangement and coordination of enzymes determines the efficiency of a multi-step reaction. These spatial arrangements can be natural (as in biomolecular complexes) or engineered with the modern methods of bio-nanotechnology. In both cases, fundamental functional tradeoffs emerge, which must be characterized to understand the optimization of such systems.
Methods from theoretical physics help to describe the functioning of these complex biomolecular systems on a quantitative level, while the biological function leads to new questions, with many parallels in the engineering disciplines. Seen from this perspective, a bacterium is a microscopic bioreactor programmed by evolution to rebuild itself from a variable set of resources and in fluctuating environments. How is this bioreactor programmed? Which strategies enable the control of a diverse set of physico-chemical processes in a way as to robustly produce a highly complex product? Quantitative analysis and modeling facilitates insight into the underlying design principles.
Recent Research Highlights
Pressure-induced Shape-shifting of Helical Bacteria
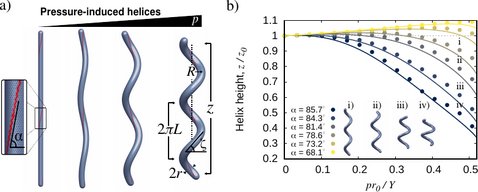
Many bacterial species are helical in form, including the widespread pathogen H. pylori. Motivated by recent experiments on H. pylori showing that cell wall synthesis is not uniform, we investigate the possible formation of helical cell shape induced by elastic heterogeneity. We show, experimentally and theoretically, that helical morphogenesis can be produced by pressurizing an elastic cylindrical vessel with helical reinforced lines. The properties of the pressurized helix are highly dependent on the initial helical angle of the reinforced region. We find that steep angles result in crooked helices with, surprisingly, reduced end-to-end distance upon pressurization. This work helps to explain the possible mechanisms for the generation of helical cell morphologies and may inspire the design of novel pressure-controlled helical actuators
Formation mechanism of thermally controlled pH gradients
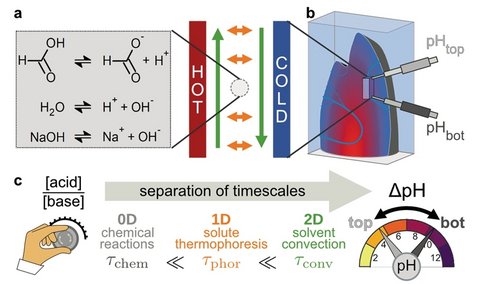
Spatial proton gradients create energy in biological systems and are likely a driving force for prebiotic systems. Due to the fast diffusion of protons, they are however difficult to create as steady state, unless driven by other non-equilibria such as thermal gradients. Here, we quantitatively predict the heat-flux driven formation of pH gradients for the case of a simple acid-base reaction system. To this end, we (i) establish a theoretical framework that describes the spatial interplay of chemical reactions with thermal convection, thermophoresis, and electrostatic forces by a separation of timescales, and (ii) report quantitative measurements in a purpose-built microfluidic device. We show experimentally that the slope of such pH gradients undergoes pronounced amplitude changes in a concentration-dependent manner and can even be inverted. The predictions of the theoretical framework fully reflect these features and establish an understanding of how naturally occurring non-equilibrium environmental conditions can drive pH gradients.
Optimal spatial allocation of enzymes as an investment problem
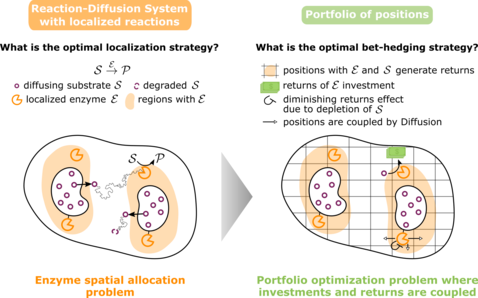
Cells face various allocation problems demanding decisions on how to distribute their finite resources. They decide which enzymes to produce at what quantity, but also where to position them. Here we focus on the spatial allocation problem of arranging enzymes such as to maximize the total reaction flux produced by them in a system with given geometry and boundary conditions. We derive an optimal allocation principle demanding that the available enzymes are distributed such that the marginal flux returns at each occupied position are equal. This ‘homogeneous marginal returns’ (HMR) criterion corresponds to a portfolio optimization of investments that globally feed back onto all payoffs. The HMR criterion allows us to analytically understand and characterize a localization-delocalization transition in the optimal enzyme distribution. Our analysis reveals the generality of the transition, and produces a practical test for the optimality of enzyme clustering by comparing the reaction flux to the influx of substrate. Based on these results, we devise an additive construction scheme, which builds up optimal enzyme arrangements systematically rather than by trial and error. Taken together, we identify a common principle in allocation problems from biology and economics, which also serves as a design principle for synthetic biomolecular systems.
MetA is a “thermal fuse” that inhibits growth and protects Escherichia coli at elevated temperatures
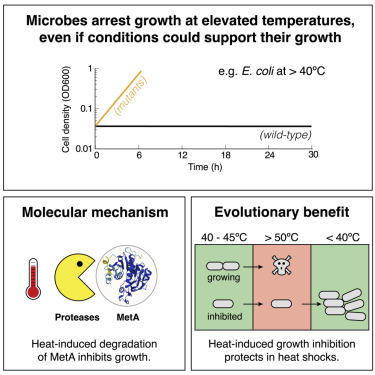
Adaptive stress resistance in microbes is mostly attributed to the expression of stress response genes, including heat-shock proteins. Here, we report a response of E. coli to heat stress caused by degradation of an enzyme in the methionine biosynthesis pathway (MetA). While MetA degradation can inhibit growth, which by itself is detrimental for fitness, we show that it directly benefits survival at temperatures exceeding 50°C, increasing survival chances by more than 1,000-fold. Using both experiments and mathematical modeling, we show quantitatively how protein expression, degradation rates, and environmental stressors cause long-term growth inhibition in otherwise habitable conditions. Because growth inhibition can be abolished with simple mutations, namely point mutations of MetA and protease knockouts, we interpret the breakdown of methionine synthesis as a system that has evolved to halt growth at high temperatures, analogous to “thermal fuses” in engineering that shut off electricity to prevent overheating.
Robust boundary formation in a morphogen gradient via cell-cell signaling
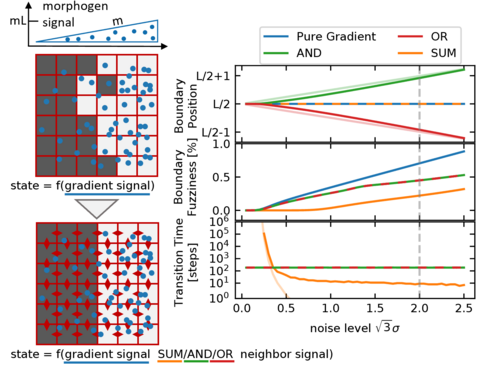
Establishing sharp and correctly positioned boundaries in spatial gene expression patterns is a central task in both developmental and synthetic biology. We consider situations where a global morphogen gradient provides positional information to cells but is insufficient to ensure the required boundary precision, due to different types of noise in the system. In a conceptual model, we quantitatively compare three mechanisms, which combine the global signal with local signaling between neighboring cells, to enhance the boundary formation process. These mechanisms differ with respect to the way in which they combine the signals by following either an AND, an OR, or a SUM rule. Within our model, we analyze the dynamics of the boundary formation process, and the fuzziness of the resulting boundary. Furthermore, we consider the tunability of the boundary position and its scaling with system size. We find that all three mechanisms produce less fuzzy boundaries than the purely gradient-based reference mechanism, even in the regime of high noise in the local signals relative to the noise in the global signal. Among the three mechanisms, the SUM rule produces the most accurate boundary. However, in contrast to the other two mechanisms, it requires noise to exit metastable states and rapidly reach the stable boundary pattern.
Emergence of Colloidal Patterns in ac Electric Fields

Suspended microparticles subjected to ac electrical fields collectively organize into band patterns perpendicular to the field direction. The bands further develop into zigzag shaped patterns, in which the particles are observed to circulate. We demonstrate that this phenomenon can be observed quite generically by generating such patterns with a wide range of particles: silica spheres, fatty acid, oil, and coacervate droplets, bacteria, and ground coffee. We show that the phenomenon can be well understood in terms of second order electrokinetic flow, which correctly predicts the hydrodynamic interactions required for the pattern formation process. Brownian particle simulations based on these interactions accurately recapitulate all of the observed pattern formation and symmetry-breaking events, starting from a homogeneous particle suspension. The emergence of the formed patterns can be predicted quantitatively within a parameter-free theory.
more research highlights ...