Physics of Pattern Formation

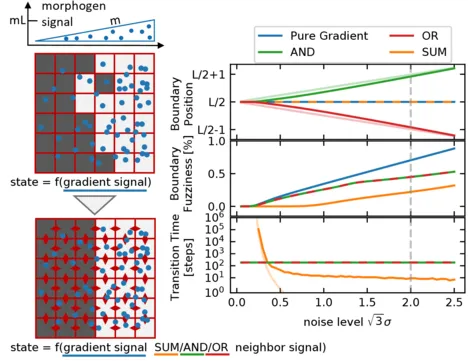
Establishing sharp and correctly positioned boundaries in spatial gene expression patterns is a central task in both developmental and synthetic biology. We consider situations where a global morphogen gradient provides positional information to cells but is insufficient to ensure the required boundary precision, due to different types of noise in the system. In a conceptual model, we quantitatively compare three mechanisms, which combine the global signal with local signaling between neighboring cells, to enhance the boundary formation process. These mechanisms differ with respect to the way in which they combine the signals by following either an AND, an OR, or a SUM rule. Within our model, we analyze the dynamics of the boundary formation process, and the fuzziness of the resulting boundary. Furthermore, we consider the tunability of the boundary position and its scaling with system size. We find that all three mechanisms produce less fuzzy boundaries than the purely gradient-based reference mechanism, even in the regime of high noise in the local signals relative to the noise in the global signal. Among the three mechanisms, the SUM rule produces the most accurate boundary. However, in contrast to the other two mechanisms, it requires noise to exit metastable states and rapidly reach the stable boundary pattern.

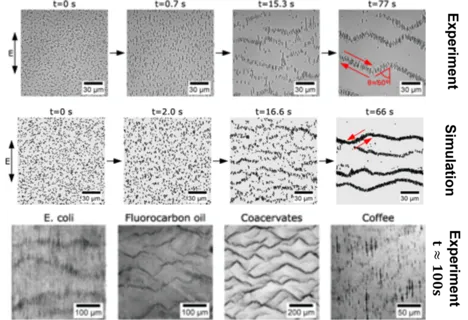
Suspended microparticles subjected to ac electrical fields collectively organize into band patterns perpendicular to the field direction. The bands further develop into zigzag shaped patterns, in which the particles are observed to circulate. We demonstrate that this phenomenon can be observed quite generically by generating such patterns with a wide range of particles: silica spheres, fatty acid, oil, and coacervate droplets, bacteria, and ground coffee. We show that the phenomenon can be well understood in terms of second order electrokinetic flow, which correctly predicts the hydrodynamic interactions required for the pattern formation process. Brownian particle simulations based on these interactions accurately recapitulate all of the observed pattern formation and symmetry-breaking events, starting from a homogeneous particle suspension. The emergence of the formed patterns can be predicted quantitatively within a parameter-free theory.

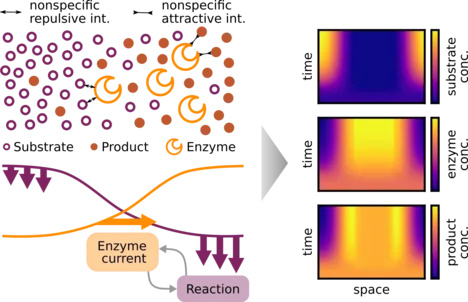
Several different enzymes display an apparent diffusion coefficient that increases with the concentration of their substrate. Moreover, their motion becomes directed in substrate gradients. Currently, there are several competing models for these transport dynamics. Here, we use mathematical modeling and numerical simulations to analyze whether the enzymatic reactions can generate a significant feedback from enzyme transport onto the substrate profile. We find that this feedback can generate spontaneous spatial patterns in the enzyme distribution, with just a single-step catalytic reaction. However, patterns are formed only for a subclass of transport models. For such models, nonspecific repulsive interactions between the enzyme and the substrate, or attractive interactions between the enzyme and the product, cause the enzyme to accumulate in regions of low substrate concentration. Reactions then amplify local substrate and product fluctuations, causing enzymes to further accumulate where substrate is low. Experimental analysis of this pattern formation process could discriminate between different transport models.

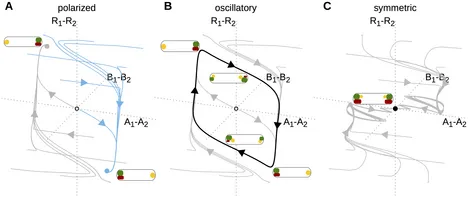
Cell polarity is key to processes such as cell growth, division, differentiation, and motility. Polarity arises from asymmetric distributions of proteins in the cell. How asymmetric patterns develop from uniform protein distributions, has been studied extensively. However, it is less clear how cells can switch such protein patterns in response to a signal. Here, we identify four qualitatively different mechanisms for how a polar protein pattern can be reversed. For each mechanism, we describe experimental signatures permitting their identification in natural systems. By providing possible regulatory circuits for these mechanisms, we also offer blueprints for synthetic implementations of switchable cell polarity, in artificial or engineered cells.

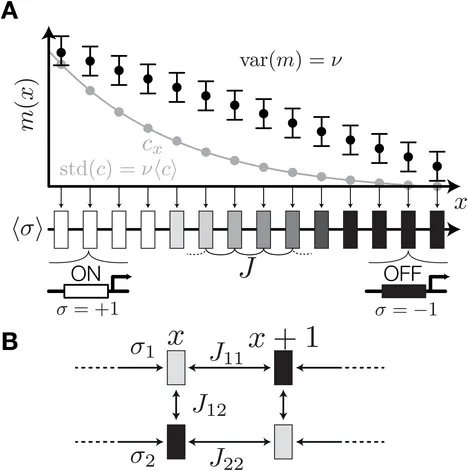
A crucial step in the early development of multicellular organisms involves the establishment of spatial patterns of gene expression which later direct proliferating cells to take on different cell fates. These patterns enable the cells to infer their global position within a tissue or an organism by reading out local gene expression levels. The patterning system is thus said to encode positional information, a concept that was formalized recently in the framework of information theory. Here we introduce a toy model of patterning in one spatial dimension, which can be seen as an extension of Wolpert’s paradigmatic “French Flag” model, to patterning by several interacting, spatially coupled genes subject to intrinsic and extrinsic noise. Our model, a variant of an Ising spin system, allows us to systematically explore expression patterns that optimally encode positional information. We find that optimal patterning systems use positional cues, as in the French Flag model, together with gene-gene interactions to generate combinatorial codes for position which we call “Counter” patterns. Counter patterns can also be stabilized against noise and variations in system size or morphogen dosage by longer-range spatial interactions of the type invoked in the Turing model. The simple setup proposed here qualitatively captures many of the experimentally observed properties of biological patterning systems and allows them to be studied in a single, theoretically consistent framework.