Molecular Dynamics of Biomolecules
Method development and applications of free-energy calculations
Free energy is the most important thermodynamic quantity because the free-energy change associated with a molecular process determines whether the process can occur spontaneously under given thermodynamic boundary conditions.
Free energies can be calculated from molecular dynamics simulation by three main approaches: (i) Alchemical methods; (ii) Endpoint methods; (iii) Pathway methods.
In our group, we develop and investigate methods to calculate free-energy differences in a computationally efficient yet accurate manner and apply free-energy calculations to biophysical research questions concerning the behavior of biomolecules in solution.
In the following, three examples are given that pertain to the three above approaches.
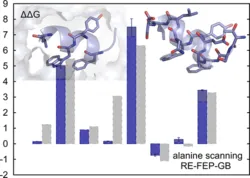
1. Rapid alchemical free-energy calculation employing a generalized Born implicit solvent model
Alchemical free-energy calculations involve "computational alchemy'', which means that atom representations are artificially altered via the use of intermediate states that do not exist in reality. In this work, the free-energy perturbation method was applied to the calculation of relative hydration free energies, relative binding free energies of a ligand-receptor system, and in silico alanine scanning of a peptide-protein complex. Computational cost was reduced by representing the solvent moiety of the systems implicitly by a generalized Born solvent model.
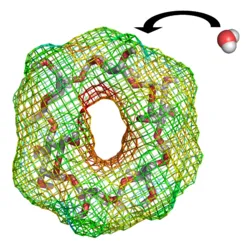
2. Rapid approximate calculation of water binding free energies in the whole hydration domain of (bio)macromolecules
Endpoint methods save computational cost by omitting the simulation of intermediate states, i.e. only the endpoint states of a molecular process are considered. In this work, water binding free energies around solute molecules were estimated from a single simulation of the hydrated solute. The underlying endpoint quantities were monitored on a three-dimensional grid around the solute, allowing a semi-quantitative thermodynamic characterization of hydration around the whole solute. Various endpoint quantities were investigated and the linear interaction energy method was considered best.
For further information read the full publication
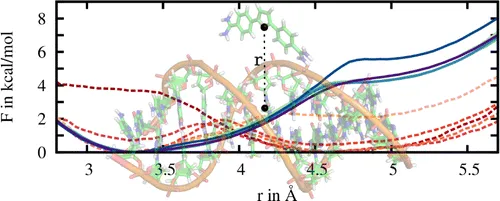
3. Adaptive biasing combined with Hamiltonian replica exchange to improve umbrella sampling free energy simulations
In pathway methods, dissociation or/and association paths involving two molecules, or intramolecular conformational changes are simulated. The free energy as a function of the reaction coordinate describing the pathway is called the potential of mean force (PMF). A common method to calculate PMFs is umbrella sampling. In this work, the PMF for the binding of a ligand to a DNA molecule was calculated. In comparison to standard PMF calculations relying solely on umbrella sampling, here convergence was significantly improved by combining the usage of adaptive biasing potentials with the Hamiltonian replica exchange scheme to exchange configurations between umbrella windows.
Twist-stretch coupling between DNA and RNA
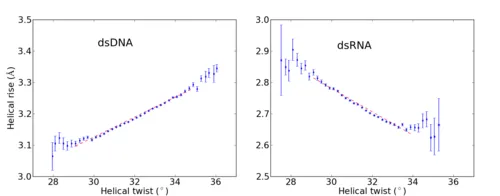
Recent single-molecule experiments pointed out that while double-stranded DNA and RNA differ only slightly in terms of their bending, twisting and stretching deformabilities, they exhibit a qualitative different twist-stretch coupling: Upon overwinding, dsDNA increases, whereas dsRNA decreases its helical extension [1]. This striking different behaviour is possibly important for understanding the packing of DNA under the influence of torsional stress and for long-range stretching deformations of helical RNA in large protein-RNA complexes triggered by a twist deformation. Employing comparative, unrestrained ~ 1 µs MD simulations we were able to trace the origin of the opposite twist-stretch coupling of dsDNA and dsRNA. During the unrestrained MD simulations of the duplexes, conformational fluctuations, which include coupled motions, are recorded. The twist-stretch coupling constant, for instance, can then simply be extracted from the correlation between helical twist and helical rise (Fig. 1). We determined a change in length per change in twist of ~ 0.032 Å/deg for dsDNA and ~ -0.037 Å/deg for dsRNA, which is in good agreement with experimental results ( 0.014 Å/deg for dsDNA, -0.024 Å/deg for dsRNA [1]).
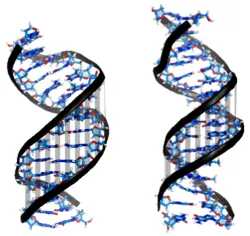
In order to figure out this opposite sign in twist-stretch coupling between dsDNA and dsRNA, correlations of all helical parameters and grooves with respect to helical twist have been studied. Upon overtwisting, dsDNA closes the minor groove (Fig. 2), thereby reducing the inclination of the base pairs with respect to the helical axis. As a consequence, the projection of the distance vectors between neighboring base pairs onto the helical axis increases, thus resulting in a more extended double helix.
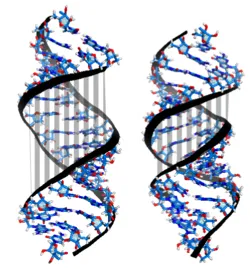
Conversely, for dsRNA, overtwisting induces the closing the major groove (Fig. 3). This is accompanied by an increase in the base pairs' inclination, which entails a reduced projection of the stacking distance between neighboring base pairs onto the helical axis and therefore a reduced helical extension.
Enzymatic nucleotide binding
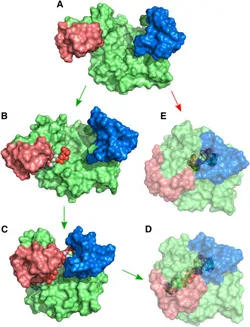
Source: [1]
Adenylate Kinase is an enzyme that catalyzes the reversible reaction ATP-Mg + AMP ↔2 ADP. The catalysis involves large scale rearrangements of two binding domains (Fig. 1, red and blue). Experiments show that the binding domains are predominantly found in open configurations when no nucleotide is bound, and in a closed configuration when the binding pocket is fully occupied. We perform atomistic Molecular Dynamics simulations with enhanced sampling methods (Replica Exchange, Umbrella Sampling) to investigate the interplay between the domain motions and nucleotide binding. From the simulations, we gain insight into how evolution has optimized the enzyme for efficient simultaneous binding of two structurally similar substrates to specific positions and how possibly non-reactive occupation of the binding pockets is avoided.
Protein–Ligand Docking Using Hamiltonian Replica Exchange Simulations with Soft Core Potentials
Abstract
Molecular dynamics (MD) simulations in explicit solvent allow studying receptor-ligand binding processes including full flexibility of the binding partners and an explicit inclusion of solvation effects. However, in MD simulations the search for an optimal ligand-receptor complex geometry is frequently trapped in locally stable non-native binding geometries. A Hamiltonian replica-exchange (H-REMD) based protocol has been designed to enhance the sampling of putative ligand-receptor complexes. It is based on softening non-bonded ligand-receptor interactions along the replicas and one reference replica under the control of the original forcefield.
Method

With modern MD algorithms and the use of accellerrated hardware (GPUs) the time scale of µs has just recently become accessible to study association processes of ligand-receptor complexes, however still with tremendous computational effort. Upon association, ligands often travel through a chain of quasi Markovian intermediate states before finally discovering the correct bound configuration. During this searching process, the ligand typically remains trapped in the intermediate states for the maior part of the simulation time, while the transition to other states happen on a faster time scale. To focus the simulation time on the exploration of ligand-receptor conformations and prevent the system of being trapped in semi-stable irrelevant states for long times a Hamiltonian based replica exchange scheme has been devised. The method accelerates the searching of possible ligand binding modes in a known binding site by scaling the non-bonded interactions of the ligand with the rest of the system. A coupling coordinate λ is introduced to connect the unmodified Hamiltonian HA of the system with a Hamiltonian HB where all non-bonded interactions of the ligand with the rest of the system are turned off (dummy ligand). Replica exchange along the λ coordinate is performed to connect the dummy ligand regime with the real force field representation HA. Ligands in higher replica (λ > 0) haved reduced interactions with the rest of the system (typically the receptor and surrounding solvent molecules) and are completely decoupled at λ = 1 resulting in an ideal gas like ligand representation. The lower the interactions between ligand and receptor, the better the ligand can diffuse in coordinate space thereby exiting potentially trapped conformations. To prevent the ligand from diffusing away from the binding site, positional restraints are applied between the center of masses of the ligand and receptor molecules.
Application
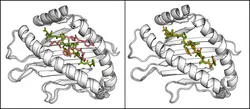
The method has been successfully applied on two different ligands both binding to the FKBP protein. For both ligands the correct binding pose was found while the ligand was mostly trapped in intermediate states during comparative MD simulations. For one ligand (FK506) the correct binding pose (compared to X-ray structures ofthe complex) was found as the largest cluster while a second ligand (SB3) reproduced the X-ray structures only in the third largest cluster strongly indicating alternative binding modes. Interestingly for the SB3 ligand alternative binding modes were also found in other studies. A second application of the H-REMD docking method was the generation of side chain configurations of small peptides in a binding site when the backbone position is approximately known. The MHC Class I protein contains a narrow cleft which can bind antigenic peptides of 8-10 residues with strongly conserved peptide backbone conformation independent of their sequence. Starting from randomized backbone and sidechain configurations of the peptide with restraint peptide backbone atoms to their conserved positions, the X-ray structure could be quickly reproduced (within less than 3 ns). A comparative MD simulation remained trapped in one single configuration.